Codigo Demical Binario
En sistemas de computación, Binary-Coded Decimal (BCD) o Decimal codificado en binario es un estándar para representar números decimales en el sistema binario, en donde cada dígito decimal es codificado con una secuencia de 4 bits. Con esta codificación especial de los dígitos decimales en el sistema binario, se pueden realizar operaciones aritméticas como suma, resta, multiplicación y división de números en representación decimal, sin perder en los cálculos la precisión ni tener las inexactitudes en que normalmente se incurre con las conversiones de decimal a binario puro y de binario puro a decimal. La conversión de los números decimales a BCD y viceversa es muy sencilla, pero los cálculos en BCD se llevan más tiempo y son algo más complicados que con números binarios puros.
Representación BCD
Cada dígito decimal tiene una representación binaria codificada con 4 bits:
Decimal: 0 1 2 3 4 5 6 7 8 9 BCD: 0000 0001 0010 0011 0100 0101 0110 0111 1000
Los números decimales, se codifican en BCD con los bits que representan sus dígitos.Por ejemplo, la codificación en BCD del número decimal 59237 es:Decimal: 5 9 2 3 7 BCD: 0101 1001 0010 0011 0111La representación anterior (en BCD) es diferente de la representación del mismo número decimal en binario puro:1110011101100101Fundamentos
En BCD cada cifra que representa un dígito decimal (0, 1,...8 y 9) se representa con su equivalente binario en cuatro bits (nibble o cuarteto) (esto es así porque es el número de bits necesario para representar el nueve, el número más alto que se puede representar en BCD). En la siguiente tabla se muestran los códigos BCD más empleados:
| Decimal | Natural | Aiken | 5 4 2 1 | Exceso 3 |
|---|---|---|---|---|
| 0 | 0000 | 0000 | 0000 | 0011 |
| 1 | 0001 | 0001 | 0001 | 0100 |
| 2 | 0010 | 0010 | 0010 | 0101 |
| 3 | 0011 | 0011 | 0011 | 0110 |
| 4 | 0100 | 0100 | 0100 | 0111 |
| 5 | 0101 | 1011 | 1000 | 1000 |
| 6 | 0110 | 1100 | 1001 | 1001 |
| 7 | 0111 | 1101 | 1010 | 1010 |
| 8 | 1000 | 1110 | 1011 | 1011 |
| 9 | 1001 | 1111 | 1100 | 1100 |
Como se observa, con el BCD sólo se utilizan 10 de las 16 posibles combinaciones que se pueden formar con números de 4 bits, por lo que el sistema pierde capacidad de representación, aunque se facilita la compresión de los números. Esto es porque el BCD sólo se usa para representar cifras, no números en su totalidad. Esto quiere decir que para números de más de una cifra hacen falta dos números BCD.
- Una forma sencilla de calcular números en BCD es sumando normalmente bit a bit, y si el conjunto de 4 bits sobrepasa el número 9, entonces se le suma un 6 (0110) en binario, para poder volver a empezar, como si hiciéramos un módulo al elemento sumante.
Desde que los sistemas informáticos empezaron a almacenar los datos en conjuntos de ocho bits (octeto), hay dos maneras comunes de almacenar los datos BCD:
- Omisión de los cuatro bits más significativos (como sucede en el EBCDIC)
- Almacenamiento de dos datos BCD; es el denominado BCD "empaquetado", en el que también se incluye en primer lugar el signo, por lo general con 1100 para el + y 1101 para el -.
De este modo, el número 127 sería representado como (11110001, 11110010, 11110111) en el EBCDIC o (00010010, 01111100) en el BCD empaquetado.
El BCD sigue siendo ampliamente utilizado para almacenar datos, en aritmética binaria o en electrónica. Los números se pueden mostrar fácilmente en visualizadores de siete segmentos enviando cada cuarteto BCD a un visualizador. La BIOS de un ordenador personal almacena generalmente la fecha y la hora en formato BCD; probablemente por razones históricas se evitó la necesidad de su conversión en ASCII.
La ventaja del código BCD frente a la representación binaria clásica es que no hay límite para el tamaño de un número. Los números que se representan en formato binarioestán generalmente limitados por el número mayor que se pueda representar con 8, 16, 32 o 64 bits. Por el contrario, utilizando BCD, añadir un nuevo dígito sólo implica añadir una nueva secuencia de 4 bits.
Conversiones de decimal A XS3 (Exceso 3)
La conversión de números decimales a exceso 3 (XS3) se realiza de la siguiente forma:
Ejemplo: Transformar el decimal 67 a XS3
Tomamos cada dígito y le sumamos 3:
6+3=9
7+3=10
Ahora cada cantidad es transformada a binario:
9=1001
10= 1010
Por lo que el resultado de la conversión a XS3 será el número 10011010
El BCD en electrónica
El BCD es muy común en sistemas electrónicos donde se debe mostrar un valor numérico, especialmente en los sistemas digitales no programados (sin microprocesador o microcontrolador).
Utilizando el código BCD, se simplifica la manipulación de los datos numéricos que deben ser mostrados por ejemplo en un visualizador de siete segmentos. Esto lleva a su vez una simplificación en el diseño físico del circuito (hardware). Si la cantidad numérica fuera almacenada y manipulada en binario natural, el circuito sería mucho más complejo que si se utiliza el BCD. Hay un programa que se llama b1411 que sirve para dividir al sistema binario en dos combinaciones. Una por ejemplo es la de sistemas digitales.
IBM y el BCD
IBM utilizó los términos decimal codificado en binario y BCD, para el código binario de seis bits con el que se podían representar números, letras mayúsculas, y caracteres especiales. Una variante del BCD fue utilizada en la mayoría de las primeras computadoras de IBM, incluyendo IBM1620 e IBM 1400. Con la introducción des System/360, el BCD fue substituido por el EBCDIC, de ocho bits.
Las posiciones de los bits, en el BCD de seis bits, generalmente fueron etiquetadas como B, A, 8, 4, 2 y 1. Para codificar los dígitos numéricos, A y B eran cero. La letra A fue codificada como (B, A, 1), etcétera.
Código Gray
|
El código binario reflejado o código Gray, nombrado así en honor del investigador Frank Gray, es un sistema de numeración binario en el que dos valores sucesivos difieren solamente en uno de sus dígitos.
El código Gray fue diseñado originalmente para prevenir señales ilegales (señales falsas o viciadas en la representación) de los switcheselectromecánicos, y actualmente es usado para facilitar la corrección de errores en los sistemas de comunicaciones, tales como algunos sistemas de televisión por cable y la televisión digital terrestre.
Nombre
El investigador de Laboratorios Bell Frank Gray inventó el término código binario reflejado cuando lo patentó en 1947, remarcando que éste "no tenía nombre reconocido aún". Él creó el nombre basándose en el hecho de que el código "puede ser construido a partir del código binario convencional por una suerte de 'proceso reflejante'".
El código fue llamado posteriormente "Gray" por otros investigadores. Dos patentes en 1953 dieron como nombre alternativo "código de Gray" para el "código binario reflejado"; uno de ellas también se refiere al código como "minimum error code" (código de error mínimo) y como "cyclic permutation code" (código de permutación cíclica).
Historia y aplicaciones prácticas
El código binario reflejado fue aplicado para acertijos matemáticos antes de ser usado para la ingeniería. El ingeniero francés Émile Baudot le dio una aplicación al código de Gray en 1878 en telegrafía, trabajo por el cual fue condecorado con la Legión de Honor.
El código Gray es atribuido en algunas ocasiones, en forma incorrecta, a Elisha Gray (en Principles of Pulse Code Modulation, K. W. Cattermole,por ejemplo.)
Hasta la primera mitad de los años 1940 los circuitos lógicos digitales se realizaban con válvulas de vacío y dispositivos electromecánicos.
Los contadores necesitaban potencias muy elevadas a la entrada y generaban picos de ruido cuando varios bits cambiaban simultáneamente. Tomando esto en cuenta, Frank Gray inventó un método para convertir señales analógicas a grupos de código binario reflejado utilizando un aparato diseñado con válvulas de vacío, con lo cual garantizó que en cualquier transición variaría tan sólo un bit.
En la actualidad, el código Gray se emplea como parte del algoritmo de diseño de los mapas de Karnaugh, los cuales son, a su vez, utilizados como "herramienta de diseño" en la implementación de circuitos combinacionales y circuitos secuenciales. La vigencia del código Gray se debe a que un diseño digital eficiente requerirá transiciones más simples y rápidas entre estados lógicos (0 ó 1), por ello es que se persiste en su uso, a pesar de que los problemas de ruido y potencia se hayan reducido con la tecnología de estado sólido de los circuitos integrados.
Utilizando el código Gray es posible también resolver el problema de las Torres de Hanói. Se puede incluso formar un ciclo hamiltoniano o un hipercubo, en el que cada bit se puede ver como una dimensión.
Debido a las propiedades de distancia de Hamming que posee el código Gray, es usado en ocasiones en algoritmos genéticos.
Motivación
Las computadoras antiguas indicaban posiciones abriendo y cerrando interruptores. Utilizando tres interruptores como entradas usando Base 2, estas dos posiciones estarían una después de la otra:
... 011 100 ...
El problema con el código binario en base 2 es que con interruptores mecánicos, es realmente difícil que todos los interruptores cambien al mismo tiempo. En la transición de los dos estados mostrados arriba, tres interruptores cambian de sitio. En el lapso en el que los interruptores están cambiando, se pueden presentar salidas de información espurias. Si las salidas mencionadas alimentan un circuito secuencial, probablemente el sistema presentará un error en entrada de datos.
El código gray resuelve este problema cambiando solamente un dígito a la vez, así que no existe este problema:
Decimal Gray Binario 0 000 000 1 001 001 2 011 010 3 010 011 4 110 100 5 111 101 6 101 110 7 100 111
tienes que tener en cuenta que para convertir de binarios a Gray los valores que deben ser sumados en base 2 toman los siguientes valores 1+1=0, 0+0=0 , 1+0=1 y 0+1=1 esta operación de forma vertical como se muestra en el siguiente ejemplo
1010 1010---- 1111
Nótese que desde el 7 podría pasar a 0 con un solo cambio de switch (el más significativo pasa a cero). Esta es la propiedad llamada "cíclica" del código de Gray.
Conversiones
| Secuencia | Binario | Gray | Secuencia | Binario | Gray | |
|---|---|---|---|---|---|---|
| 1000 | ||||||
| 1001 | ||||||
| 1010 | ||||||
| 1011 | ||||||
| 1100 | ||||||
| 1101 | ||||||
| 1110 | ||||||
| 1111 |
Base 2 a Gray
Para convertir un número binario (en Base 2) a código Gray, simplemente se le aplica una operación XOR con el mismo número desplazado un bit a la derecha, sin tener en cuenta el acarreo.
Ejemplo: 1010 (Base 2) a gray
1010 1010---- 1111
Otros ejemplos 0111(Base 2) a gray :
0111 0111------ 0100
110101010001 110101010001------------ 101111111001
Gray a Base 2
Definimos un vector conteniendo los dígitos en gray y otro vector destinado a contener los dígitos en Base 2
conteniendo los dígitos en gray y otro vector 
destinado a contener los dígitos en Base 2- es el dígito que se encuentra en el extremo izquierdo de la representación en código gray
es el dígito que se encuentra en el extremo izquierdo de la representación en código gray- es el dígito de mayor peso y que se encuentra en el extremo izquierdo en la representación en Base 2
es el dígito de mayor peso y que se encuentra en el extremo izquierdo en la representación en Base 2
Luego resulta que: con la excepción de que , la cual se puede resumir como:
con la excepción de que 
, la cual se puede resumir como:
El dígito de más a la izquierda en Base 2 es igual al dígito de más a la izquierda en código gray
Ejemplo Con el número en código Gray.
en código Gray.
Lo primero es decir que: , por lo que para este caso: . Luego siguiendo con el algoritmo: resulta que:
. Luego siguiendo con el algoritmo: 
Esto da como resultado
Código Aiken
CD Aiken – Código BCD Exceso 3
Se recomienda leer el tutorial sobre el Sistema binario antes de iniciar la lectura de este tutorial.
El código BCD Aiken es un código similar alcódigo BCD natural pero con los “pesos” o “valores” distribuidos de una manera diferente. En el códigoBCD natural, los pesos son: 8 – 4 – 2 – 1, en el código Aiken la distribución es: 2 – 4 – 2 – 1.
La razón de esta codificación es la de conseguir simetría entre ciertos números. Ver la simetría en el código Aiken corresponiente a los decimales: 4 y 5, 3 y 6, 2 y 7, 1 y 8, 0 y 9.
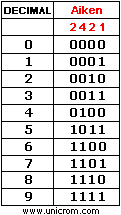
Analizar la tabla que se muestra en la figura anterior. Cada cifra es el complemento a 9 de la cifra simétrica en todos sus dígitos.(los “1” se vuelven “0” y los “0” se vuelven “1”). Ejemplo: 3 (0011) y 6 (1100).Tomar en cuenta los nuevos “pesos” en este código. El código Aiken es muy útil para realizar operaciones de resta y división.
Código Exceso 3
El código Exceso 3 se obtiene sumando “3” a cada combinación del código BCD natural. Ver la tabla inferior. El código exceso 3 es un código en donde la ponderación no existe (no hay “pesos” como en el código BCD natural y código Aiken). Al igual que el código Aiken cumple con la misma característica de simetría. Cada cifra es el complemento a 9 de la cifra simétrica en todos sus dígitos.
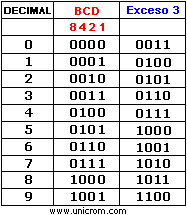
Ver la simetría en el código exceso 3 correspondiente a los decimales: 4 y 5, 3 y 6, 2 y 7, 1 y 8, 0 y 9. Es un código muy útil en las operaciones de resta y división.
